Simple Genetic Algorithm

Whether it’s building maple seed shaped drones or inventing Velcro based on burdock burrs, nature has always been a great inspiration for humans.

It goes without saying that optimization algorithms optimize for some kind of goal or target metric. Evolution is no different. Natural selection in the real world optimizes for survival on Earth. In fact, each and every life form on Earth is a solution generated by evolution’s algorithm, which evolves a population of individuals over generations, optimizing for survival. Give it enough time (4.5 billion years), and you get humans, although we have yet to pass certain extinction tests that have wiped out other species in the past, but I’m optimistic.

In this post we’ll loosely draw inspiration from evolution to build a simple genetic algorithm.

Our two main classes will be an Individual and a Population, and populations are made up of individuals. Our individuals will be made up of 10 initially random integers between 0 and 100. The goal will be to get the sum of those 10 numbers to equal 900, and that’ll be the measure of how fit an individual is.

We’ll initialize a population with a population size of 100 individuals, where each individual will be randomly initialized. Then we’ll evolve the population to find an optimal solution.

Here are the basic steps for the evolving part:

Select the fittest (sum is closest to 900) individuals to be the parents of the next generation. In this case a fitness of 0 will be the best because fitness is abs(900 — sum(individual.numbers))
We’ll randomly select some of the non-fittest individuals to be parents as well. This increases our chance of finding a global optimum. Then we’ll breed or crossover the selected parents, creating new individuals, that we’ll call the children . Instead of randomly initializing the children, we’ll base them on the parents. When creating children, there’ll be a chance that the child will have a random mutation of it’s numbers.
The parents and the children will form part of the next generation.
Calculate the average population fitness. Rinse and repeat.
When we hit an average population fitness of 0 (or close to it) we’ll stop evolving. Normally it’s more intuitive to have a higher fitness be better than a lower fitness, in our case our convention is that lower fitness is better.

import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import random

class Individual(object):

    def __init__(self, numbers=None, mutate_prob=0.01):
        if numbers is None:
            self.numbers = np.random.randint(101, size=10)
        else:
            self.numbers = numbers
            # Mutate
            if mutate_prob > np.random.rand():
                mutate_index = np.random.randint(len(self.numbers) - 1)
                self.numbers[mutate_index] = np.random.randint(101)

    def fitness(self):
        """
            Returns fitness of individual
            Fitness is the difference between
        """
        target_sum = 900
        return abs(target_sum - np.sum(self.numbers))

class Population(object):

    def __init__(self, pop_size=10, mutate_prob=0.01, retain=0.2, random_retain=0.03):
        """
            Args
                pop_size: size of population
                fitness_goal: goal that population will be graded against
        """
        self.pop_size = pop_size
        self.mutate_prob = mutate_prob
        self.retain = retain
        self.random_retain = random_retain
        self.fitness_history = []
        self.parents = []
        self.done = False

        # Create individuals
        self.individuals = []
        for x in range(pop_size):
            self.individuals.append(Individual(numbers=None,mutate_prob=self.mutate_prob))

    def grade(self, generation=None):
        """
            Grade the generation by getting the average fitness of its individuals
        """
        fitness_sum = 0
        for x in self.individuals:
            fitness_sum += x.fitness()

        pop_fitness = fitness_sum / self.pop_size
        self.fitness_history.append(pop_fitness)

        # Set Done flag if we hit target
        if int(round(pop_fitness)) == 0:
            self.done = True

        if generation is not None:
            if generation % 5 == 0:
                print("Episode",generation,"Population fitness:", pop_fitness)

    def select_parents(self):
        """
            Select the fittest individuals to be the parents of next generation (lower fitness it better in this case)
            Also select a some random non-fittest individuals to help get us out of local maximums
        """
        # Sort individuals by fitness (we use reversed because in this case lower fintess is better)
        self.individuals = list(reversed(sorted(self.individuals, key=lambda x: x.fitness(), reverse=True)))
        # Keep the fittest as parents for next gen
        retain_length = self.retain * len(self.individuals)
        self.parents = self.individuals[:int(retain_length)]

        # Randomly select some from unfittest and add to parents array
        unfittest = self.individuals[int(retain_length):]
        for unfit in unfittest:
            if self.random_retain > np.random.rand():
                self.parents.append(unfit)

    def breed(self):
        """
            Crossover the parents to generate children and new generation of individuals
        """
        target_children_size = self.pop_size - len(self.parents)
        children = []
        if len(self.parents) > 0:
            while len(children) < target_children_size:
                father = random.choice(self.parents)
                mother = random.choice(self.parents)
                if father != mother:
                    child_numbers = [ random.choice(pixel_pair) for pixel_pair in zip(father.numbers, mother.numbers)]
                    child = Individual(child_numbers)
                    children.append(child)
            self.individuals = self.parents + children

    def evolve(self):
        # 1. Select fittest
        self.select_parents()
        # 2. Create children and new generation
        self.breed()
        # 3. Reset parents and children
        self.parents = []
        self.children = []

if __name__ == "__main__":
    pop_size = 1000
    mutate_prob = 0.01
    retain = 0.1
    random_retain = 0.03

    pop = Population(pop_size=pop_size, mutate_prob=mutate_prob, retain=retain, random_retain=random_retain)

    SHOW_PLOT = True
    GENERATIONS = 5000
    for x in range(GENERATIONS):
        pop.grade(generation=x)
        pop.evolve()

        if pop.done:
            print("Finished at generation:", x, ", Population fitness:", pop.fitness_history[-1])
            break

    # Plot fitness history
    if SHOW_PLOT:
        print("Showing fitness history graph")
        matplotlib.use("MacOSX")
        plt.plot(np.arange(len(pop.fitness_history)), pop.fitness_history)
        plt.ylabel('Fitness')
        plt.xlabel('Generations')
        plt.title('Fitness - pop_size {} mutate_prob {} retain {} random_retain {}'.format(pop_size, mutate_prob, retain, random_retain))
        plt.show()

This of course is a super simplified version of a more complex program we could build. For example, we could have different species competing with each other, and we can have the chance of mutation be property of a species, etc. Having just the right mutation chance could make the difference between one species winning over another.

Once we have the main code nailed down, it’s fun to play around with the parameters and look at how long it takes to achieve an optimal solution:

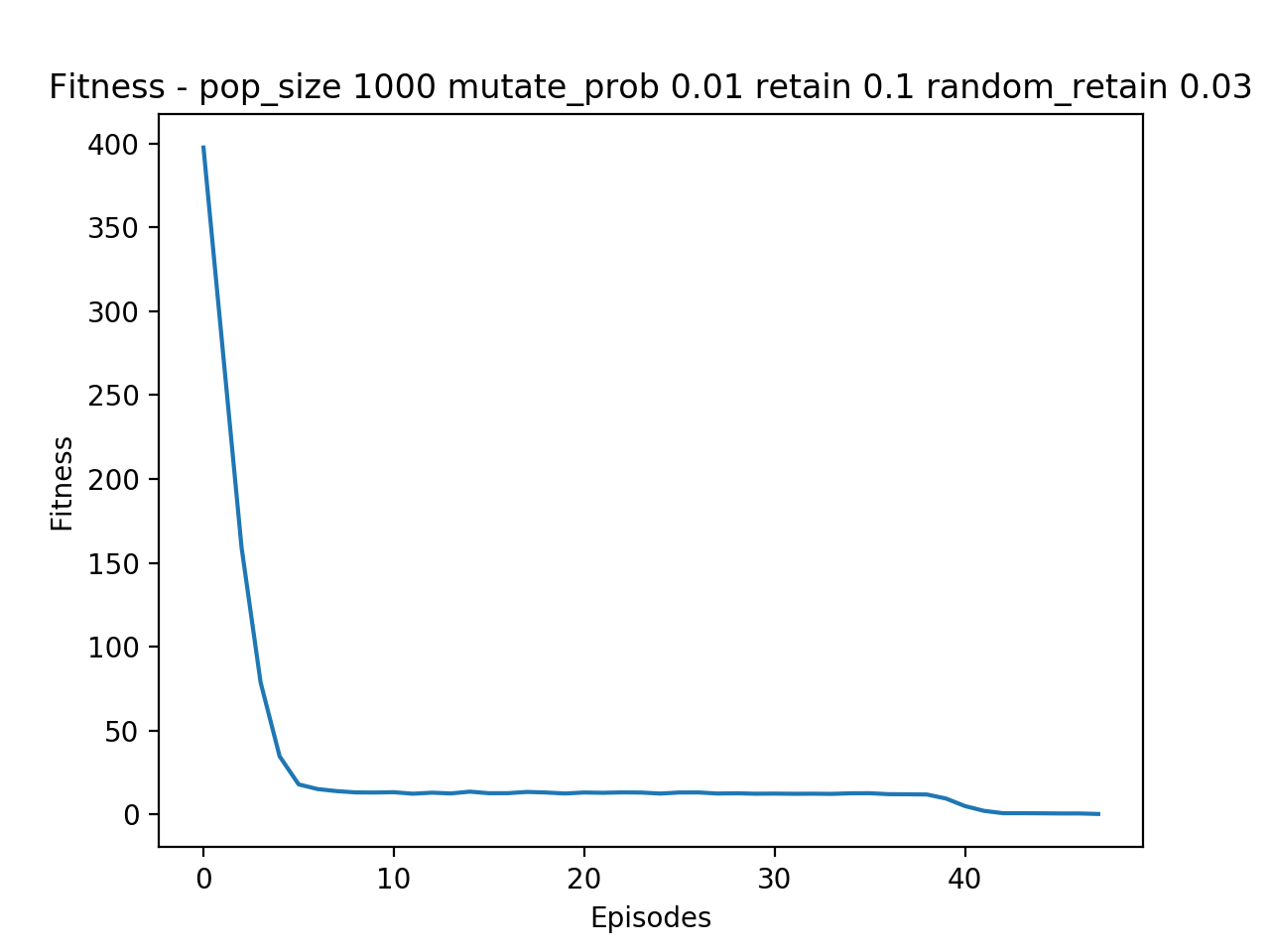
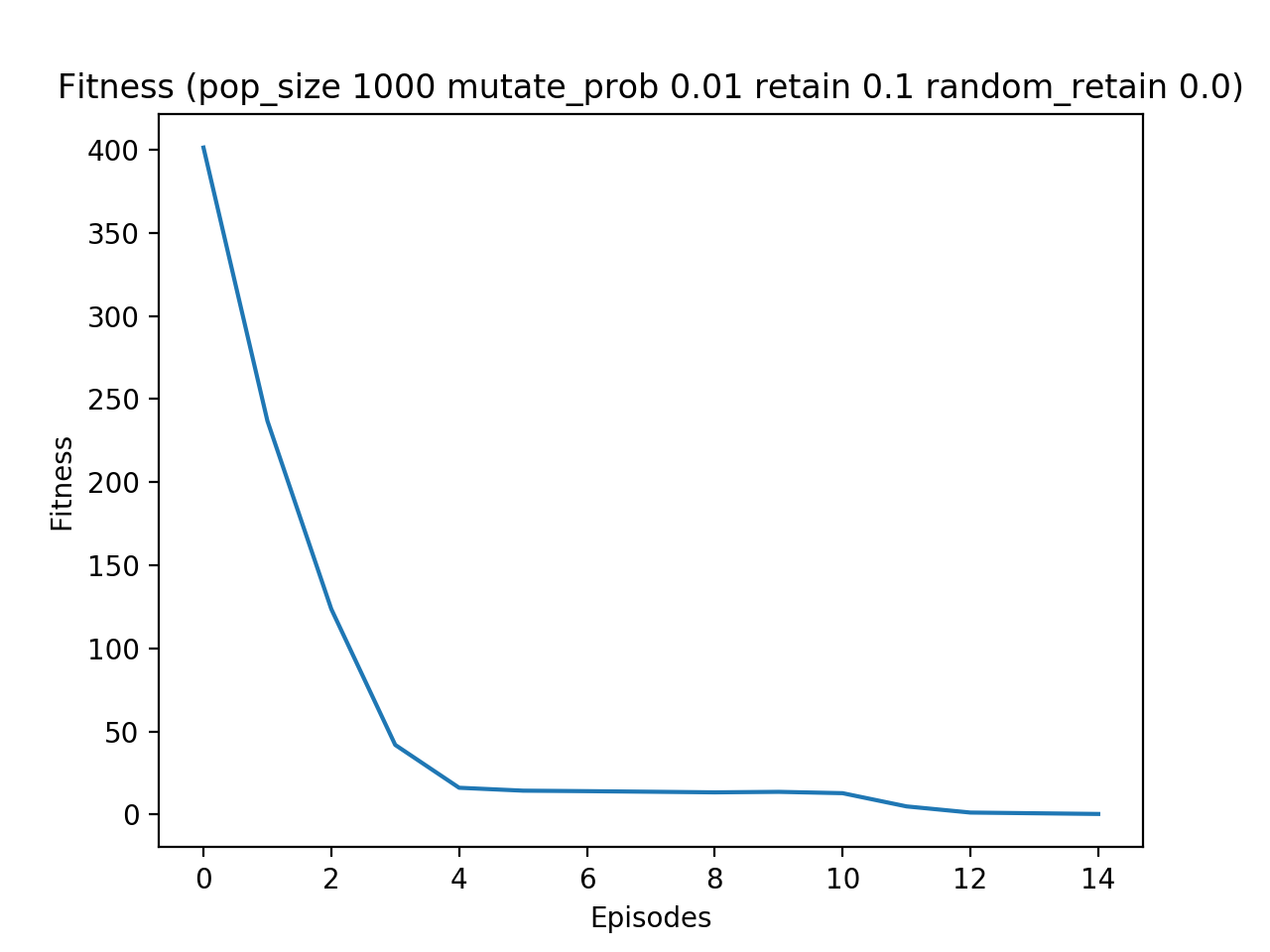
Fitness 1 Fitness 2

Here’s a link to the repo: https://github.com/gabrielgarza/simple-genetic-algorithm

To run this code, do in your terminal:

git clone git@github.com:gabrielgarza/simple-genetic-algorithm.git
cd simple-geneteic-algorightm
python evolve.py

We can use these kinds of genetic algorithms to build really cool things, such as evolving a neural network’s hyperparameters leading to a very efficient search of optimal parameters. Thanks for reading and let me know if you have any feedback :) Happy holidays!