In this post we’ll build a Reinforcement Learning model using a Policy Gradient Network. We’ll use Tensorflow to build our model and use Open AI’s Gym to measure our performance against the Lunar Lander game.

Reinforcement Learning

I’ve been amazed by the power of deep reinforcement learning algorithms. There are several powerful methods such as Deep Q Learning, popularized by Deep Mind with their Atari Pong player in 2015, and in this post we’ll go through my favorite RL method, Policy Gradients.

There are three main branches in machine learning: Supervised Learning (learning from labeled data), Unsupervised Learning (learning patterns from unlabeled data), and Reinforcement Learning (discovering data/labels through exploration and a reward signal). Reinforcement Learning is a lot like supervised learning, except not only do you start without labels, but without data too. This is why I believe RL is so important, as it allows us start learning from zero experience, much like we humans do as we’re born with zero experience. The human reward function has been tuned for millions of years to optimize for survival, that is, for every action we take in the world we get a positive reward if its expected value increases our chance of survival or a negative reward if it lowers our chance of survival (think pleasure when you eat or pain when you fall down). As we go along in life we learn to take actions that are more likely to lead to positive rewards. If you are interested in RL I highly recommend checking out David Silver’s course and Fei-Fei Li’s Stanford course.

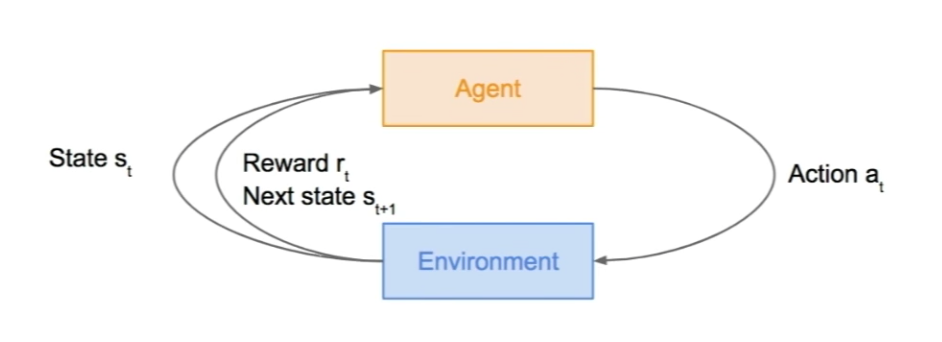
In RL, an agent interacts with it’s environment through a sequence of events:

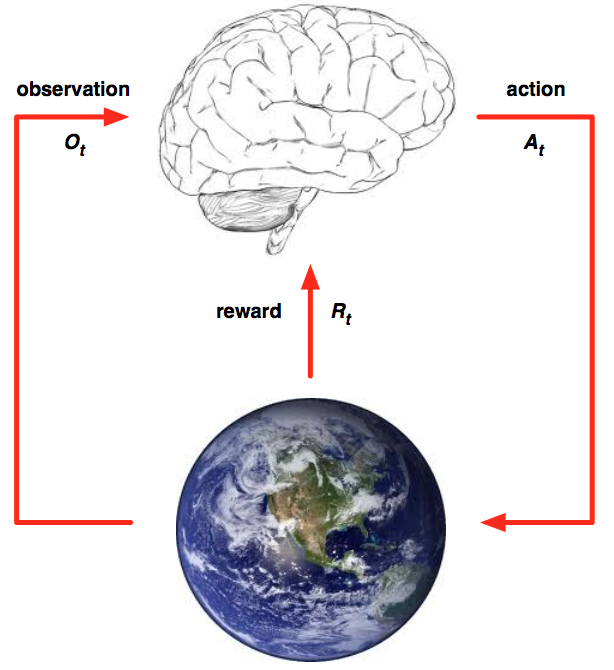
Agent — Environment from David Silver’s Course
Agent — Environment from David Silver’s Course

The sequence is:

  • Agent observes the environment’s initial state s
  • Agent chooses an action a and receives a reward r and a new state s_ from the environment
State, Action, Reward sequence from Stanford’s Fei-Fei Li Course
State, Action, Reward sequence from Stanford’s Fei-Fei Li Course

OpenAI’s Gym gives us a great way to train and test out our RL models through games, which are great for RL, as we have clear actions (left, right, etc.), states (could be position of players or pixels of screen, etc.), and rewards (points).

Our objective is to learn a policy or model that will maximize expected rewards. Concretely, we need to train a neural network (the policy) to predict the action, given a state, that will maximize future rewards!

Lunar Lander

We’ll use one of my favorite OpenAI Gym games, Lunar Lander, to test our model. The goal, as you can imagine, is to land on the moon! There are four discrete actions available: do nothing, fire left orientation engine, fire main engine, fire right orientation engine. The state is the coordinates and position of the lander. The reward is a combination of how close the lander is to the landing pad and how close it is to zero speed, basically the closer it is to landing the higher the reward. There are other things that affect the reward such as, firing the main engine deducts points on every frame, moving away from the landing pad deducts points, crashing deducts points, etc. This reward function is determined by the Lunar Lander environment. The game or episode ends when the lander lands, crashes, or flies off away from the screen.

Policy Gradient Network

To approximate our policy, we’ll use a 3 layer neural network with 10 units in each of the hidden layers and 4 units in the output layer:

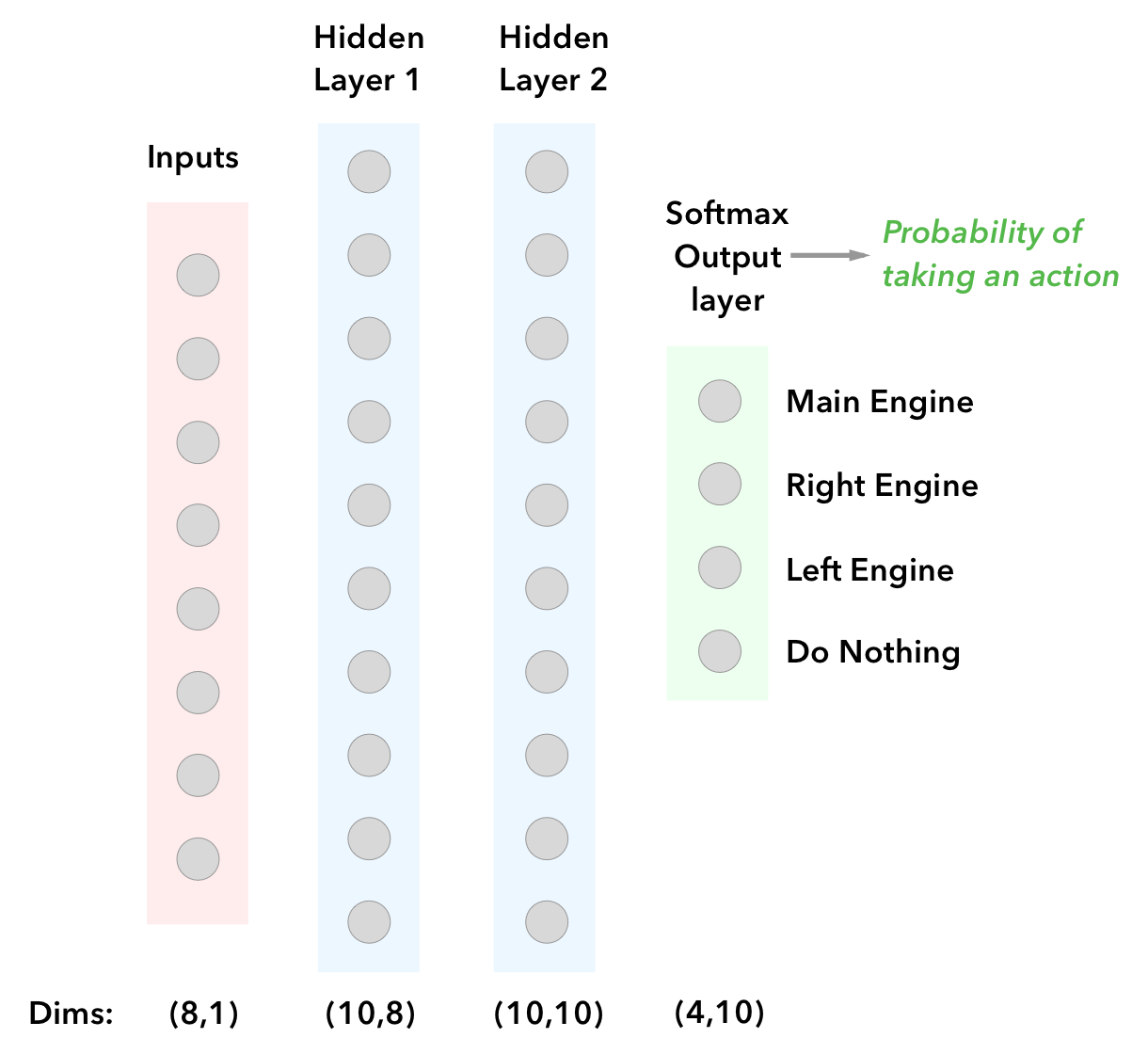
Policy Network Architecture
Policy Network Architecture

Network in Tensorflow:

def build_network(self):
        # Create placeholders
        with tf.name_scope('inputs'):
            self.X = tf.placeholder(tf.float32, shape=(self.n_x, None), name="X")
            self.Y = tf.placeholder(tf.float32, shape=(self.n_y, None), name="Y")
            self.discounted_episode_rewards_norm = tf.placeholder(tf.float32, [None, ], name="actions_value")
# Initialize parameters
        units_layer_1 = 10
        units_layer_2 = 10
        units_output_layer = self.n_y
        with tf.name_scope('parameters'):
            W1 = tf.get_variable("W1", [units_layer_1, self.n_x], initializer = tf.contrib.layers.xavier_initializer(seed=1))
            b1 = tf.get_variable("b1", [units_layer_1, 1], initializer = tf.contrib.layers.xavier_initializer(seed=1))
            W2 = tf.get_variable("W2", [units_layer_2, units_layer_1], initializer = tf.contrib.layers.xavier_initializer(seed=1))
            b2 = tf.get_variable("b2", [units_layer_2, 1], initializer = tf.contrib.layers.xavier_initializer(seed=1))
            W3 = tf.get_variable("W3", [self.n_y, units_layer_2], initializer = tf.contrib.layers.xavier_initializer(seed=1))
            b3 = tf.get_variable("b3", [self.n_y, 1], initializer = tf.contrib.layers.xavier_initializer(seed=1))
# Forward prop
        with tf.name_scope('layer_1'):
            Z1 = tf.add(tf.matmul(W1,self.X), b1)
            A1 = tf.nn.relu(Z1)
        with tf.name_scope('layer_2'):
            Z2 = tf.add(tf.matmul(W2, A1), b2)
            A2 = tf.nn.relu(Z2)
        with tf.name_scope('layer_3'):
            Z3 = tf.add(tf.matmul(W3, A2), b3)
            A3 = tf.nn.softmax(Z3)
# Softmax outputs, we need to transpose as tensorflow nn functions expects them in this shape
        logits = tf.transpose(Z3)
        labels = tf.transpose(self.Y)
        self.outputs_softmax = tf.nn.softmax(logits, name='A3')
with tf.name_scope('loss'):
            neg_log_prob = tf.nn.softmax_cross_entropy_with_logits(logits=logits, labels=labels)
            loss = tf.reduce_mean(neg_log_prob * self.discounted_episode_rewards_norm)  # reward guided loss
with tf.name_scope('train'):
            self.train_op = tf.train.AdamOptimizer(self.lr).minimize(loss)

The input vector is the state X that we get from the Gym environment. These could be pixels or any kind of state such as coordinates and distances. The lunar Lander game gives us a vector of dimensions (8,1) for our state, and we’ll map those to the probability of taking a certain action.

Loss function

For our loss function we’ll use a softmax cross entropy, which gives us the negative log probability of our actions as an output. We’ll then multiply this by our reward (reward guided loss), so we can update our parameters in a way that encourages actions that lead to high rewards and discourages actions that lead to low rewards. We’ll use the Adam Optimizer to train our model. Our loss will look something like this:

# Using Tensorflow
neg_log_prob = tf.nn.softmax_cross_entropy_with_logits(logits=logits, labels=labels)
loss = tf.reduce_mean(neg_log_prob * discounted_episode_rewards_norm)
tf.train.AdamOptimizer(learning_rate).minimize(loss)

Discounting future rewards and normalizing them (subtracting mean then dividing by standard deviation) helps to reduce variance. There are ways we could improve our loss function, by crafting a better Advantage Function. For example, add a baseline to our rewards or using methods such as the Actor Critic, which combines Policy Gradients with Deep Q-learning, would help to reduce variance. In our case, our Advantage Function is simply our discounted and normalized rewards.

Training

Where is the training data coming from? How do we get the logits and labels in the code above? Initially, we don’t have any data. for every game we play (episode) we will be saving the state, action, and reward for every step in the sequence, you can think of each of these steps as a training example. This will serve as our training data. Our input vector X is the state. Our logits are the outputs Z3 (before softmax) of the network and our labels Y are the actions we took.

Algorithm

We’ll play 5,000 episodes (games) total and for each episode here are the step’s we’ll follow:

  1. Get the state from the environment.
  2. Feed forward our policy network to predict the probability of each action we should take. We’ll sample from this distribution to choose which action to take (i.e. toss a biased coin).
  3. Receive the reward and the next state state_ from the environment for the action we took.
  4. Store this transition sequence of state, action, reward, for later training.
  5. Repeat steps 1–4. If we receive the done flag from the game it means the episode is over.
  6. Once the episode is over, we train our neural network to learn from our stored transitions using our reward guided loss function.
  7. Play next episode and repeat steps above! Eventually our agent will get good at the game and start getting some high scores.

Results

Initially the agent is not very good at landing, it’s basically taking random actions:

After several hundred episodes the agent starts to learn how to fly!

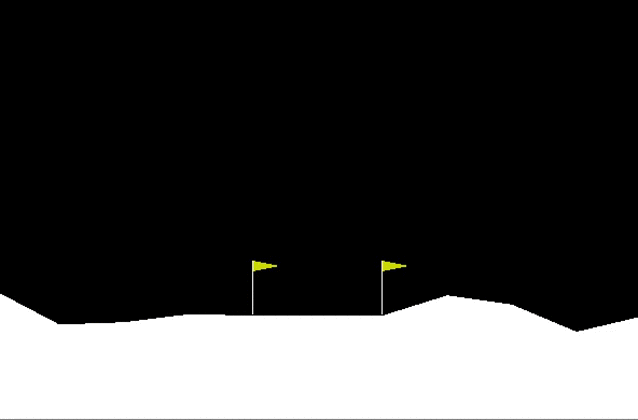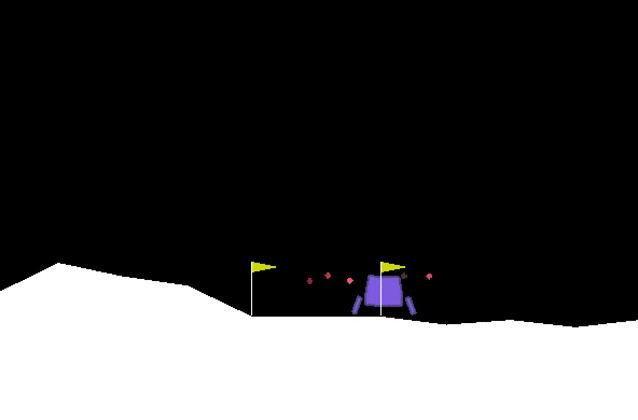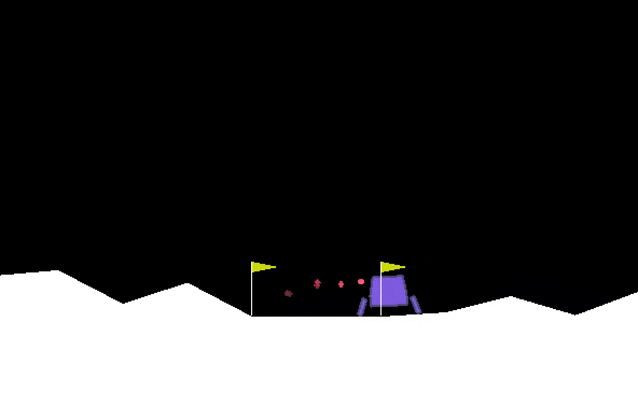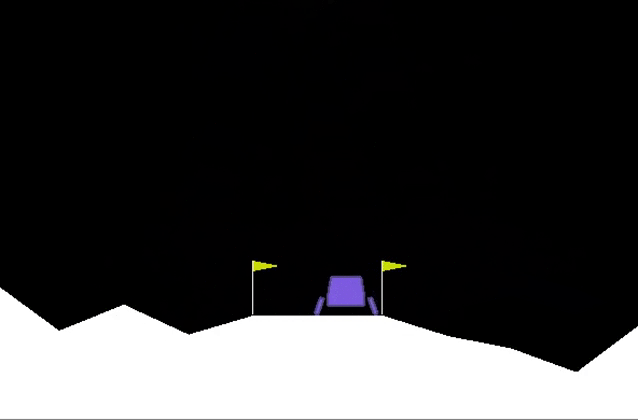
Eventually after about 3 thousand episodes, the agent learns how to land in the landing zone!

Conclusions

  1. Pretty amazing we can accomplish the results above with less than 200 lines of code and training on a regular Macbook Pro.
  2. The agent started out with 0 data and 0 labels. Through trial and error, the agent took actions in the environment and received a reward for each action. We then trained the agent on that data, adjusting the weights to encourage actions that lead to higher rewards and discourage actions that lead to low rewards. Eventually, the agent learned how to land in the landing zone!
  3. How do we know if an action at time-step 3 will lead to a better reward in time-step 300? This is called the credit assignment problem and leads to high variance. You can over come this through lots of training and crafting a better advantage function (the scalar or reward that multiplies your labels to encourage or discourage actions).
  4. We can improve our model and reduce variance (and fix credit assignment problem) by introducing a better advantage function. For example, we could use a baseline or try out the Actor Critic method, in which the Critic (another neural network) would estimate the advantage function.
  5. I’ve gotten great results applying this same model to other games in the Gym environment, such as CartPole or MountainCar. It’s exciting to think how one day this kind of generalizable learning can be applied to robots that we can train to do things for us (kind of like training a dog or other pet).

Full Source Code: https://github.com/gabrielgarza/openai-gym-policy-gradient